回溯法

2 回溯法——用递归来解决嵌套层数的问题 

1
2
3
4

给定一个不含重复数字的数组 nums ，返回其 所有可能的全排列 。你可以 按任意顺序 返回答案。

示例 输入：nums = [1,2,3]
	输出：[[1,2,3],[1,3,2],[2,1,3],[2,3,1],[3,1,2],[3,2,1]]

​ 肯定可以用暴力方法来解决, 但是当nums数组数量多了的时候, 例如50, 我们需要写 50 层 for循环, 这是个不可能完成的任务.

​ 回溯法模板, 因为一般来说, 用回溯法解决的问题是一个集合, 所以不能直接返回结果, 因此, backtrack 需要将 结果集合( 一个多维数组 )传入进去来维护他, 还有所有的选择, 以及路径.

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13

result = []
def backtrack(res, 路径, 选择列表):
    if 满⾜结束条件:
        res.add(路径)
        return

    for 选择 in 选择列表:
        判断是否需要剪枝, 也就是将不符合题意的循环删除
        
        #在递归之前做出选择，在递归之后撤销刚才的选择
        做选择
        backtrack(路径, 选择列表)
        撤销选择

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20

# 伪代码分析
给定一个不含重复数字的数组 nums ，返回其 所有可能的全排列 。你可以 按任意顺序 返回答案。

示例 输入：nums = [1,2,3]
	输出：[[1,2,3],[1,3,2],[2,1,3],[2,3,1],[3,1,2],[3,2,1]]
    
def backtrack(res, nums, track):
    if nums.size() == track.size():
        res.add(track)
        return

    for num in nums:
        # 判断是否需要剪枝, 也就是将不符合题意的循环删除
        # 在这个问题中, nums 在 track中重复
        if num in track: continue;
        
        #在递归之前做出选择，在递归之后撤销刚才的选择
        track.push_back(num)
        backtrack(res, nums, track)
        track.pop_back(num)

46_全排列

给定一个不含重复数字的数组 nums ，返回其 所有可能的全排列 。你可以 按任意顺序 返回答案。

示例

输入：nums = [1,2,3] 输出：[[1,2,3],[1,3,2],[2,1,3],[2,3,1],[3,1,2],[3,2,1]]

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26

    void backtrack(vector<vector<int> > &res, vector<int> &nums, vector<int> &track, vector<int> &flag){
        if(track.size() == nums.size()){
            res.push_back(track);
            return;
        }
        for(int i =0; i<nums.size(); ++i){
            if(flag[i] == 1) continue;
            track.push_back(nums[i]);
            flag[i] =1;
            backtrack(res, nums, track, flag);
            flag[i] =0;
            track.pop_back();
        }
    } 

    vector<vector<int>> permute(vector<int>& nums) {
        int len = nums.size();
        vector<int> track, flag(len, 0);
        //flag is the element is used
        vector<vector<int> > res;


        backtrack(res, nums, track, flag);

        return res;
    }

77_组合

给定两个整数 n 和 k，返回范围 [1, n] 中所有可能的 k 个数的组合。 你可以按 任何顺序 返回答案。 输入：n = 4, k = 2 输出： [ [2,4],[3,4],[2,3],[1,2],[1,3],[1,4], ]

//解题思路: 一般我们在进行答案的搜索的时候, 都是从小的开始, 先1, 然后2, 并且只找比他大的数 [1,2],[1,3],[1,4],[2,3],[2,4], [3,4]

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31

vector<vector<int>> combine(int n, int k) {
    vector<int> track;
    vector<vector<int> > res;
    backtrack(res, n, k, 1, track);
    return res;

}

//----------------------------错误解法1------------------------------
//输出了   [[1,1],[1,2],[1,3],[1,4],[2,1],[2,2],[2,3],[2,4],[3,1],[3,2],[3,3],[3,4],[4,1],[4,2],[4,3],[4,4]]
void backtrack(vector<vector<int> > &res, int n, int k, int start, vector<int> &track){
    if(track.size() == k) {
        res.push_back(track);
        for_each(track.begin(), track.end(), [&](int x){cout<< x;});
        cout<< endl;
        return;
    }
    
	//for循环 第一句话, 标志着树的 每层 从哪里开始
    for(int i =1; i<=n; ++i){
        track.push_back(i);
        //递归调用标志着 下一层树
        backtrack(res, n, k, start+1, track);
        track.pop_back();
    }
}
//-----------其实就是start没有用上------
//回溯树如下图所示, 以后不对的时候, 就画图看一下
							[]
	[1]  		[2] 		 [3],,,,,,,,,,,,,,,,,,,,,,,,,,
[1][2][3][4]

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17

//----------------------------正确解法1------------------------------
void backtrack(vector<vector<int> > &res, int n, int k, int start, vector<int> &track){
    if(track.size() == k) {
        res.push_back(track);
        for_each(track.begin(), track.end(), [&](int x){cout<< x;});
        cout<< endl;
        return;
    }
    
	//for循环 第一句话, 标志着树的 每层 从哪里开始
    for(int i =start; i<=n; ++i){
        track.push_back(i);
        //递归调用标志着 下一层树
        backtrack(res, n, k, i+1, track);
        track.pop_back();
    }
}

216_组合总和3

找出所有相加之和为 n 的 k 个数的组合，且满足下列条件：

  • 只使用数字1到9
  • 每个数字 最多使用一次

返回 所有可能的有效组合的列表 。该列表不能包含相同的组合两次，组合可以以任何顺序返回。

示例 1:

1
2
3
4
5

输入: k = 3, n = 7
输出: [[1,2,4]]
解释:
1 + 2 + 4 = 7
没有其他符合的组合了。

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25

vector<vector<int>> combinationSum3(int k, int n) {
    vector< vector<int> > res;
    vector<int> track;
    //vector<int> flag(10,0);

    backtrack(res, k, n, track, 1, 0);
    return res;

}

void backtrack(vector<vector<int> > &res, int k, int n,vector<int> &track, int start, int sum){
    // sum 是树节点 的总和
    if(track.size() == k && sum == n){
        res.push_back(track);
        return;
    }


    for(int i = start; i<10; ++i){
        track.push_back(i);
        backtrack(res, k, n, track, i+1, sum +i);
        track.pop_back();

    }
}

1

algorithm_回溯_backtrack_3_总结
  • 回溯总是和递归联系在一起的
  • 要仔细 分析 回溯 树 每一层是从哪个元素开始的

回溯和递归

3.1 回溯总是和递归联系在一起的 

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13

result = []
def backtrack(res, 路径, 选择列表):
    if 满⾜结束条件:
        res.add(路径)
        return

    for 选择 in 选择列表:
        判断是否需要剪枝, 也就是将不符合题意的循环删除
        
        #在递归之前做出选择，在递归之后撤销刚才的选择
        做选择
        backtrack(路径, 选择列表)
        撤销选择

​ 回溯其实就是不断的调用自身, 直至满足结束条件

3.2 要仔细 分析 回溯 树 每一层是从哪个元素开始的

方法还是上次说过的 画图

3.2.1 全排列——-每个元素不重复

给定一个不含重复数字的数组 nums ，返回其 所有可能的全排列 。你可以 按任意顺序 返回答案。

示例

输入：nums = [1,2,3] 输出：[[1,2,3],[1,3,2],[2,1,3],[2,3,1],[3,1,2],[3,2,1]]

分析:

1
2
3
4

                            []
        [1]            [2]           [3],,,,,,,,,,,,,,,,,,,,,,,,,,
    [2]    [3]   [4]
[3]   [4]

​ 第一层是全部( 1 2 3 4 ), 第二层是缺一个, 第三层是缺两个

​ 总结起来就是每个元素不重复

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11

//for循环分析
for(int i =0; i<nums.size(); ++i){
    //flag 代表了 是否被使用过
    if(flag[i] == 1) continue;
    track.push_back(nums[i]);
    flag[i] =1;
    //下一层 代表 也是 从头开始
    backtrack(res, nums, track, flag);
    flag[i] =0;
    track.pop_back();
}

3.2.2 组合

给定两个整数 n 和 k，返回范围 [1, n] 中所有可能的 k 个数的组合。 你可以按 任何顺序 返回答案。 输入：n = 4, k = 2 输出： [ [2,4],[3,4],[2,3],[1,2],[1,3],[1,4], ]

//解题思路: 一般我们在进行答案的搜索的时候, 都是从小的开始, 先1, 然后2, 并且只找比他大的数 [1,2],[1,3],[1,4],[2,3],[2,4], [3,4]

1
2
3
4

                    []
   [1]               [2]       ....
[2] [3] [4]
[3] 空  空

​ 从小的开始, 先1, 然后2, 并且只找比他大的数, 有了3 就不在加入 2

1
2
3
4
5
6
7

//for循环 第一句话, 标志着树的 每层 从哪里开始
for(int i =start ; i<=n; ++i){
    track.push_back(i);
    // 下一层树 从哪里开始, 如果顺序有制约, 那么一定和i有关
    backtrack(res, n, k, i+1, track);
    track.pop_back();
}

3.2.3 组合总和

给你一个 无重复元素 的整数数组 candidates 和一个目标整数 target ，找出 candidates 中可以使数字和为目标数 target 的 所有 不同组合 ，并以列表形式返回。你可以按 任意顺序 返回这些组合。

candidates 中的 同一个 数字可以 无限制重复被选取 。如果至少一个数字的被选数量不同，则两种组合是不同的。

对于给定的输入，保证和为 target 的不同组合数少于 150 个。

1
2
3
4
5
6

输入：candidates = [2,3,6,7], target = 7
输出：[[2,2,3],[7]]
解释：
2 和 3 可以形成一组候选，2 + 2 + 3 = 7 。注意 2 可以使用多次。
7 也是一个候选， 7 = 7 。
仅有这两种组合。

1
2
3
4
5
6

for(int i = start ;i<can.size(); i++){
    track.push_back(can[i]);
    //下一层 还是从本层的 这个元素开始, 因为这个元素可以使用多次
    backtrack(res, can, target, track, sum+can[i], i);
    track.pop_back();
}

3.2.4 组合总和3

找出所有相加之和为 n 的 k 个数的组合，且满足下列条件：

  • 只使用数字1到9
  • 每个数字 最多使用一次

返回 所有可能的有效组合的列表 。该列表不能包含相同的组合两次，组合可以以任何顺序返回。

示例 1:

1
2
3
4
5

输入: k = 3, n = 7
输出: [[1,2,4]]
解释:
1 + 2 + 4 = 7
没有其他符合的组合了。

1
2
3
4
5
6

for(int i = start; i<10; ++i){
    track.push_back(i);
	//下一层元素从 下一个元素 后面开始, 因为 元素 不能重复, 
    backtrack(res, k, n, track, i+1, sum +i);
    track.pop_back();
}

3.2.5 电话号码的字母组合

给定一个仅包含数字 2-9 的字符串，返回所有它能表示的字母组合。答案可以按 任意顺序 返回。

给出数字到字母的映射如下（与电话按键相同）。注意 1 不对应任何字母。

img

1
2
3
4
5
6
7
8
9

//一个元素 映射为 一个数组 的元素
vector<char> amap = _map(ch);
for(int i = 0; i<amap.size(); ++i){
    ch2 = amap[i];
    track.push_back(ch2);
    //下一层和 这一层没关系
    backtrack(res, digits, track);
    track.pop_back();
}

去重 

1

algorithm_回溯_backtrack_4_去重

40_组合总和2(重要, 涉及去重,去重使用了排序)

给定一个候选人编号的集合 candidates 和一个目标数 target ，找出 candidates 中所有可以使数字和为 target 的组合。

candidates 中的每个数字在每个组合中只能使用 一次 。

**注意：**解集不能包含重复的组合。

示例 1:

1
2

输入: candidates = [10,1,2,7,6,1,5], target = 8,
输出:  [   [1,1,6],[1,2,5],[1,7],[2,6]  ]

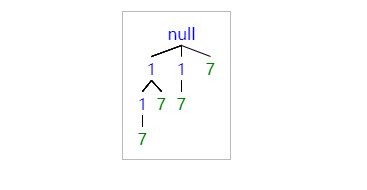
​ 集合(数组candidates)有重复元素,但还不能有重复的组合.

去重 时, 遇事不决, 直接排序

image-20220924111421337

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80

//------------------  V-1.0 -------------------------
//  期望输出   [   [1,1,6],[1,2,5],[1,7],[2,6]  ]
//  实际输出   [[1,2,5],[1,7],[1,6,1],[2,6],[2,1,5],[7,1]]

vector<vector<int>> combinationSum2(vector<int>& candidates, int target) {
    vector<vector<int> > res;
    vector<int> track;

    backtrack(res, candidates, target, track, 0, 0);
    return res;

}

void backtrack(vector<vector<int> > &res, vector<int> &can, int target, vector<int> &track, int sum, int start){
    if(sum == target){
        res.push_back(track);
        return;
    }
    if(track.size() >= can.size() || sum> target) return;

    for(int i = start; i< can.size(); ++i){
        
        track.push_back(can[i]);
        backtrack(res, can, target, track, sum+can[i], i+1);
        track.pop_back();
    }
}
    
//----------------------- V-2.0 ----------------------
// 回溯树如下
//                                 []
//     [1] ,,,, [1](重复了),,,,, 
// [1](依旧可以选) 

// 因为 已经搜索过了, 你再搜索, 就会重复 
// 既然需要 每一行 去重, 那么, 先排序, 在for循环里面判断一下前面用没用过不就行了?
// 很遗憾, 实际的结果是 [[1,2,5],[1,7],[2,6]]
// 期望输出      [   [1,1,6],[1,2,5],[1,7],[2,6]  ]
// 虽然 确实去掉了1,7 和7,1的重复, 但是缺少了 1, 1, 6 的组合
// 问题出在了哪里?
// 实际的情况是, 我们平时使用for循环时(比如使用的方法 是 遍历法 ), 总是横向的, 横向的意思是回溯树有同一个父亲
// for(){for(){for(){}}}
// 但是因为 回溯法使用了递归, for循环又会竖向使用, (回溯树中的父子关系)
sort(candidates.begin(), candidates.end());
for(int i = start; i< can.size(); ++i){
    if(i>0 && can[i] == can[i-1]) continue;
    track.push_back(can[i]);
    backtrack(res, can, target, track, sum+can[i], i+1);
    track.pop_back();
}

//----------------------- V1.0 ----------------------
vector<vector<int>> combinationSum2(vector<int>& candidates, int target) {
    vector<vector<int> > res;
    vector<int> track, flag(candidates.size(), 0);

    sort(candidates.begin(), candidates.end());
    backtrack(res, candidates, target, track, 0, 0, flag);
    return res;

}

void backtrack(vector<vector<int> > &res, vector<int> &can, int target, vector<int> &track, int sum, int start, vector<int> &flag){
    if(sum == target){
        res.push_back(track);
        return;
    }
    if(track.size() >= can.size() || sum> target) return;

    for(int i = start; i< can.size(); ++i){
        //  比较反直觉, 没有用过 才表示 是同一层重复
        if(i>0 && can[i] == can[i-1] &&flag[i-1]==0 )
            continue;
        flag[i] =1;
        track.push_back(can[i]);
        backtrack(res, can, target, track, sum+can[i], i+1, flag);
        track.pop_back();
        flag[i] =0;
    }
}
Algorithm
Licensed under CC BY-NC-SA 4.0
最后更新于 Oct 13, 2024 21:15 +0800
© 2020 - 2024 Example Person
使用 Hugo 构建
主题 Stack 由 Jimmy 设计